Можливі три випадки розташування прямих у просторі:
1) прямі присікаються, т. Е. Мають спільну точку;
2) прямі паралельні, т. Е. Не мають спільної точки, але лежать в одній площині;
3) прямі схрещуються, т. Е. Чи не лежать в одній площині, т. Е. Через них не можна провести площину.
Коли прямі перетинаються, на епюрі точки перетину їх однойменних проекцій на горизонтальній і фронтальній площинах знаходяться на одному перпендикуляр до осі х.
Розглянемо прямі I і II, які перетинаються в точці А (рис. 26). Спроектуємо обидві прямі на горизонтальну площину. Якщо врахувати, що точка А належить обом прямим, то її проекція а буде належати також і обидва проекція прямих. 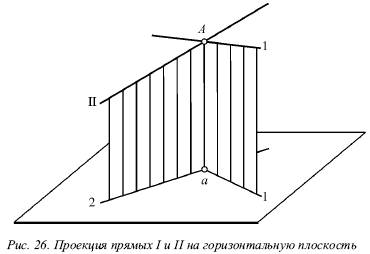
Схожа картина буде і на фронтальній площині, т. Е. Ці точки перетину однойменних проекцій а й а є проекціями деякої точки А, і тому вони повинні лежати на одному перпендикуляр до осі х. Точно так же буде вірним і зворотне твердження: якщо на епюрі точки перетину однойменних проекцій прямих на дві площини (горизонтальну і фронтальну) лежать на одному перпендикуляр до осі х, то ці прямі перетинаються.
Нехай проекції прямих I до II (рис. 27) підкоряються цій умові. 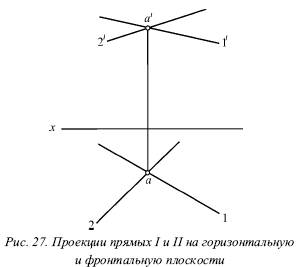
Тоді точки перетину їх однойменних проекцій можна Рассматриваються як проекції деякої точки в просторі. Позначимо точку перетину горизонтальних проекцій 1 і 2 буквою а, а точку перетину фронтальних проекцій 1 і 2 - буквою а. Вже згадана точка А знаходиться і на прямий I, і на прямій II. Тобто вона є їхньою спільною точкою, в якій перетинаються ці прямі.
Пряме твердження справедливо у всіх випадках без винятку. Зворотне ж твердження можна застосувати в тому випадку, якщо хоча б одна з прямих профільна.
Коли прямі паралельні
, На епюрі їх однойменні проекції паралельні (рис. 28). 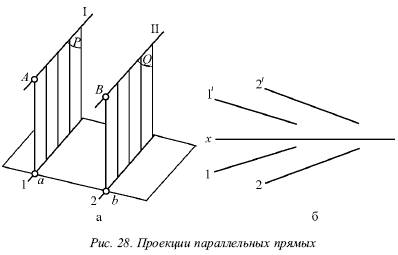
Насправді, площині Р і Q, що проектують прямі I і II на горизонтальну площину, паралельні, так як в кожній з цих площин можна вказати дві пересічні прямі, паралельні двом пересічним прямим другої площини, т. Е. Пряма I паралельна прямій II, і проектує промінь Аа паралельний променю Вb. Але дві паралельні площини Р і Q перетнуть горизонтальну площину. В результаті цього утворюються дві паралельні прямі 1 і 2, т. Е. Горизонтальні проекції прямих I і II паралельні між собою.
Аналогічно можна довести, що і будь-які інші однойменні проекції обох прямих також будуть паралельні один одному.
Вірно і зворотне твердження: прямі паралельні, якщо на епюрі їх однойменні проекції паралельні. 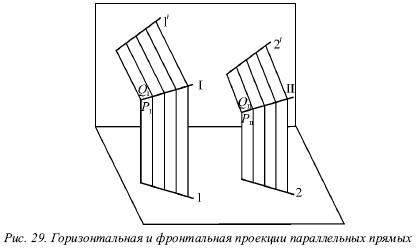
Якщо відомо, що горизонтальні і фронтальні проекції прямих I і II паралельні, буде справедливо наступне: 1 || 2 і 1 || 2 (рис. 29).
В цьому випадку можна сказати, що площині Р I і Р II, що проектують прямі I і II на горизонтальну площину, паралельні, так як в цих площинах можна вказати по парі пересічних відповідно паралельних прямих (прямі 1 і 2 і проектують промені). Аналогічно площині QI і Q II будуть паралельні.
Пряма I знаходиться в перетині площин Р I і QI, а пряма II - в перетині площин РII QII. Звідси отримуємо, що пряма I паралельна площині РII, тому що знаходиться в площині, їй паралельної. Однак пряма I паралельна і площині Q II. Тому пряма I паралельна лінії перетину площин Р II і Q II, т. Е. Прямої II. 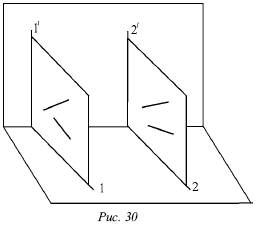
Доказ зворотного твердження не має сенсу для профільних прямих. Це пояснюється тим, що тоді замість двох площин, що проектують пряму на горизонтальну і фронтальну площини, існує тільки одна, двічі проектує площину (рис. 30).
Видно, що незалежно від розташування двох профільних прямих I і II в просторі їх горизонтальні і фронтальні проекції завжди паралельні (або зливаються).
Інша по темі
Велике Об'єднання в математиці
Був малий не промах, а став, як чума. Виною всьому - теорема Ферма: Не може ніяк він її довести, Уайлса приклад не дає йому спати. Фернандо Гувеа На цей раз ніяких сумнівів в доведенні не було. Дві статті загальним обсяг ...


